Datentypen in SINGULAR und Ringe

SINGULAR arbeitet mit einer ganzen Reihe von unterschiedlichen Strukturen, die als verschiedene Datentypen vorliegen. Will man ein Objekt in SINGULAR definieren, sprich eine Variable einführen, so ist es notwendig, ihr von Beginn an einen Datentyp zuzuweisen.

In SINGULAR sind die Datentypen, bis auf die Ausnahmen string, int, intvec und intmat, von einer Metastruktur abhängig, dem sogenannten Ring, über dem sie leben. (Es ist Teil der Vorlesung Lineare Algebra, zu definieren, was ein Ring ist, und welche Ringe in Singular zur Verfügung stehen.) Will man eine Rechnung in SINGULAR durchführen, ist es deshalb stets unabdingbar, zunächst den Ring zu definieren, über dem man arbeitet. Für die Lineare Algebra werden wir zu Beginn mit den folgenden Ringdefinitionen auskommen:

ring r=0,(x),lp;	Die Menge der Polynome in der Variablen x mit Koeffizienten in den rationalen Zahlen $\mathbbm Q$.
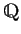ring r=(0,a,b),(x,y,z),lp;	Die Menge der Polynome in den Variablen x,y,z, wobei die Koeffizienten rationale Ausdrücke in den Variablen a und b sind. Natürlich können statt a, b bzw. x, y, z auch beliebige andere Variablen stehen. Wesentlich ist, daß die Variablen in der ersten Klammer im Nenner von Brüchen auftauchen dürfen, die in der zweiten Klammer nicht.

Wir sehen also, daß wir zunächst über den rationalen Zahlen 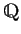$\mathbbm Q$ rechnen werden. Reelle Zahlen als Dezimalzahlen (floating point numbers) oder gar komplexe Zahlen werden wir erst zu einem späteren Zeitpunkt zur Verfügung haben. Im folgenden geben wir ein Liste der in Singular verfügbaren Datentypen, und wir geben auch jeweils ein Beispiel an, indem wir eine Variable des entsprechenden Typs definieren und ihr einen Wert zuweisen, durch den Operator =. Für die Lineare Algebra werden wir zunächst mit den ersten acht Typen auskommen. Die anderen sind nur der Vollständigkeit halber aufgeführt worden.

int i=1;	Der Datentyp integer repräsentiert die Maschinenzahlen (= ganze Zahlen). Außerdem werden Wahrheitswerte (= boolean) als integers repräsentiert, 0 = FALSE, 1 = TRUE.
string s="Hallo";	strings sind beliebige Zeichenketten. Stets durch Anführungszeichen eingegrenzt.
intvec iv=1,2,3,4;	Ein Vektor aus integers.
intmat im[2][3]=1,2,3,4,5,6;	Eine Matrix mit 2 Zeilen und 3 Spalten mit integer-Einträgen, hier $\left(\begin{array}{rrr}1&2&3\\ 4&5&6\end{array}\right)$.
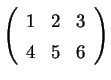ring R=(0,a),(x,y),lp;	Der Ring ${\mathbbm Q}(a)[x,y]$ mit lexikographischer Ordnung. Für weitere Erläuterungen konsultiere man das Handbuch [#!GPS99!#].
number n=4/6;	numbers sind die Elemente des Körpers, der dem Ring zugrunde liegt. Bei ring r=0,(x),lp; also die rationalen Zahlen, bei ring r=(0,a),(x),lp; auch Brüche von Polynomen in a mit ganzzahligen Koeffizienten, etwa $\frac{a^2+1}{a-1}$.
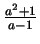list l=n,iv,s;	Eine Liste kann Objekte ganz unterschiedlicher Typen enthalten. Auf den zweiten Eintrag von l kann durch l[2] zugegriffen werden.
matrix m[2][3]=1,2,3,4,5,6;	Eine Matrix mit 2 Zeilen und 3 Spalten, bei der die Einträge entweder vom Typ poly oder vom Typ number sind, wie hier $\left(\begin{array}{rrr}1&2&3\\ 4&5&6\end{array}\right)$.
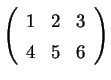vector v=[1,2,3];	Ein Vektor im Modul R3. Sind die Einträge sämtlich number, können wir ihn aber auch als Vektor über dem Grundkörper auffassen.
proc	Der Datentyp procedure ist in Kapitel ausführlich besprochen.
poly f=x2+2x+1;	Ein Polynom in den Veränderlichen des Rings mit numbers als Koeffizienten, hier f=x2+2x+1. Beachte, daß Zahlen vor den Monomen als Koeffizienten interpretiert werden, wohingegen SINGULAR Zahlen nach einzelnen Variablen als Exponenten interpretiert.
ideal i=f,x3;	Das von f und x3 erzeugt Ideal in R.
qring Q=i;	Der Quotientenring R/i.
map g=R,x;	Die Abbildung von R nach Q, die durch 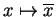$x\mapsto \overline{x}$ definiert wird.
module mo=v,[x,x2,x+1];	Der von den Vektoren v und (x,x2,x+1)t in R3 aufgespannte Modul.
def j;	Will man sich zum Zeitpunkt der Definition einer Variablen noch nicht festlegen, welchen Typ sie haben soll, so definiert man sie als def. Die erste Zuweisung, mit der der Variablen ein Wert zugewiesen wird, legt dann auch den Datentyp fest.
link	Für den Datentyp link verweisen wir auf das Handbuch [#!GPS99!#].
resolution	Für den Datentyp resolution verweisen wir auf das Handbuch [#!GPS99!#].

Auf den ersten Blick mag es erscheinen, als ob die Matrizen im und m identisch seien. Für SINGULAR ist das jedoch nicht der Fall, da sie von unterschiedlichem Typ sind!

Will man mit Dezimalzahlen rechnen, also gleichsam den Grundkörper 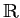$\R$ zur Verfügung haben, so muß man in der Definition des Rings die ``Charakteristik'' 0 durch real ersetzen (bzw. (real,50), wenn man mit 50 Nachkommastellen rechnen will), z. B. 

ring r=(real,10),x,lp;

Sogar die komplexen Zahlen sind verfügbar, indem man real durch complex ersetzt. i bezeichnet dann die imaginäre Einheit, d. h. die Quadratwurzel aus -1.