Level spacings of the quantised kicked rotator


The kicked rotator is invariant under parity, i.e. the inversion of both q and p (cf. the clearly visible center of inversion in the phase space plots). The quantum eigenphases corresponding to different eigenvalues of the parity operator have to be viewed as independent spectra. Thus also for large values of the kicking strength (e.g. k=10.0, below), i.e. for classically chaotic dynamics, we do not observe GOE-statistics but a level spacing density P(s) which can be described by the independent superposition of two GOE spectra, given by (`2GOE')
P(s) = pi/8 s exp(-pi/16 s2) erfc(sqrt(pi)/4 s) + 1/2 exp(-pi/8 s2).

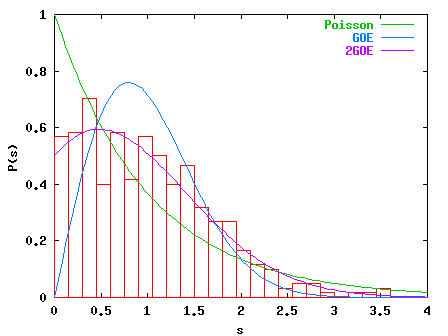
P(s) for k=10.0

Therefore, in the following we only take into account eigenphases (always 400) corresponding to states with even parity. The distribution of level spacings should be compared to the corresponding phase space plots.

For k=0.0 (below), i.e. for rotations of the torus, the quantised (non-)kicked rotator shows degeneracies yielding non-generic level spacing statistics.

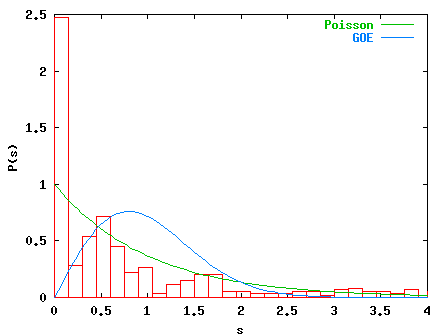
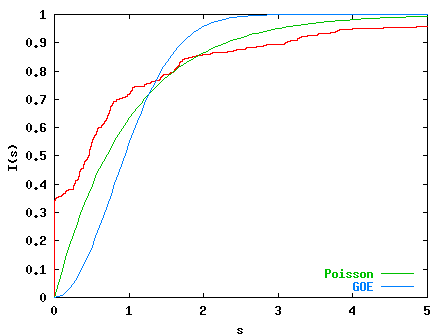
P(s) for k=0.0 I(s) for k=0.0

A small perturbation (k=0.05, below) destroys the degeneracies and thus we observe generic level spacing statistics close to Poisson.

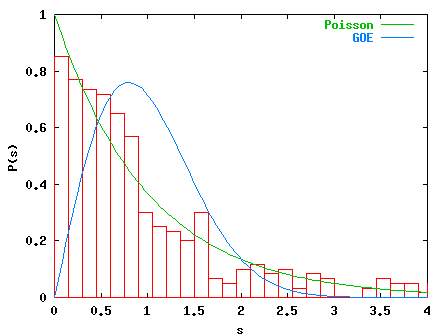
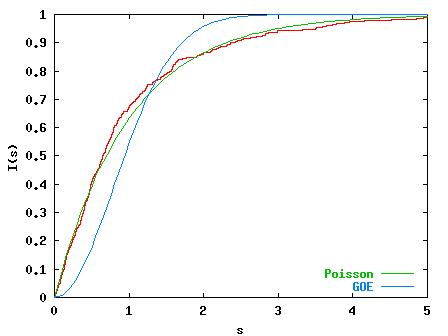
P(s) for k=0.05 I(s) for k=0.05

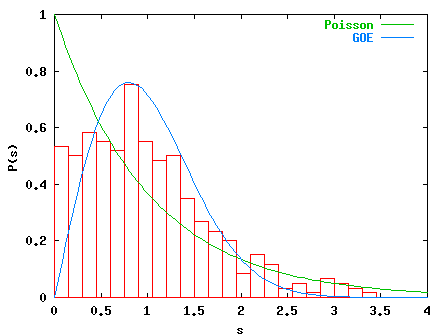
For k=2.0 (below) the statistics is between Poisson and GOE, corresponding to the mixed classical phase space with regular and chaotic regions.

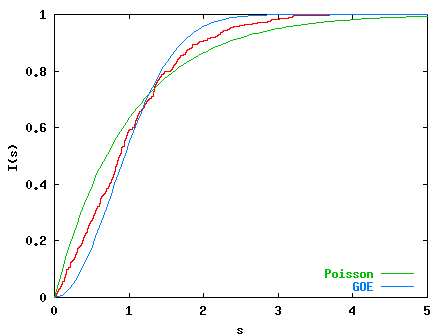
P(s) for k=2.0 I(s) for k=2.0

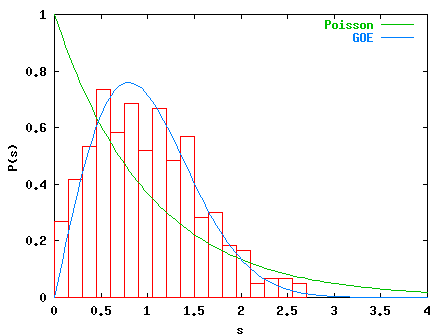
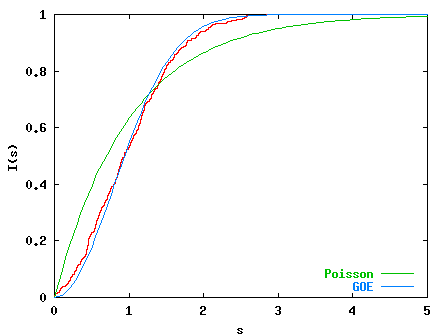
For k=7.0 (below) we observe agreement with the GOE which is to be understood as a fingerprint of the `chaotic' phase space (with only small integrable islands left).

P(s) for k=7.0 I(s) for k=7.0

Valid HTML 4.01! Last modified: Jul 17 2001
Stefan Keppeler ( stefan.keppeler@physik.uni-ulm.de)