Stability of some fixed/periodic points of the standard map


In problem 3 we have found two fixed points of the standard map at (p,q)=(0,0) and (0,pi), respectively, and a periodic orbit of period two given by the points (pi,0) and (pi,pi).

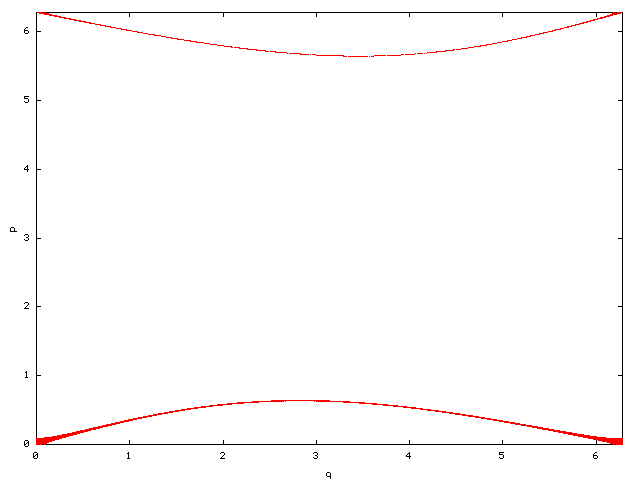
The fixed point (0,0) is unstable for all k>0. This is illustrated by iterating points in the vicinity of (0,0) for k=0.1 which spread to a band (below).

orbits around (0,0) for k=0.1

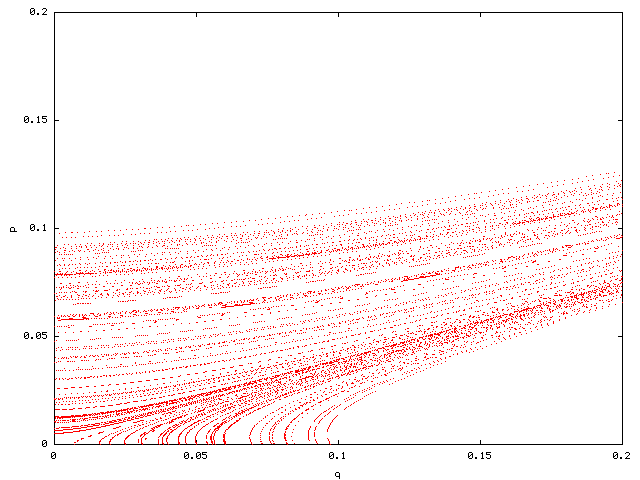
Magnifying the area around (0,0) we can observe the stable and unstable directions (below).

orbits around (0,0) for k=0.1, details

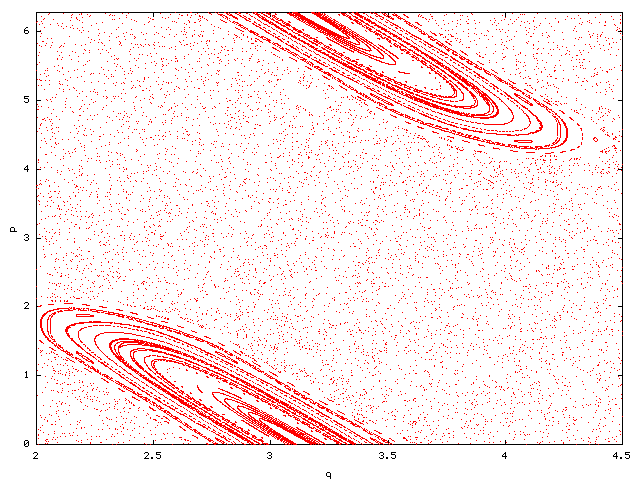
The fixed point (0,pi) is stable for k=3.9 (below).

orbits around (0,pi) for k=3.9

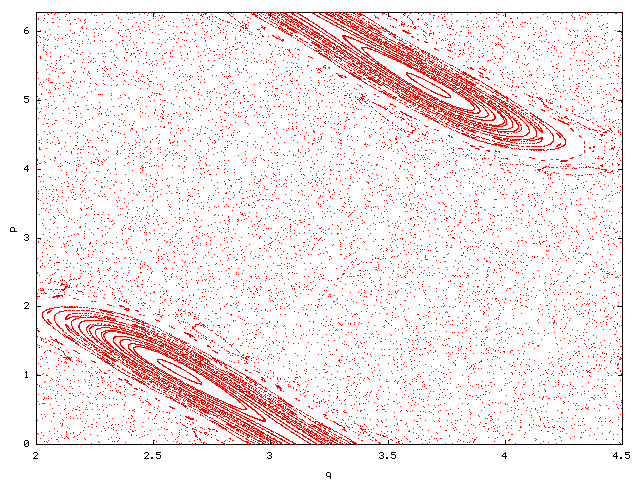
For k=4.2 (below) the fixed point (0,pi) has become unstable but we have created a stable periodic orbit of period two in the vicinity - this process is known as period doubling.

orbits around (0,pi) for k=4.2

For k=1.9 the periodic orbit [(pi,0),(pi,pi)] is stable (below).

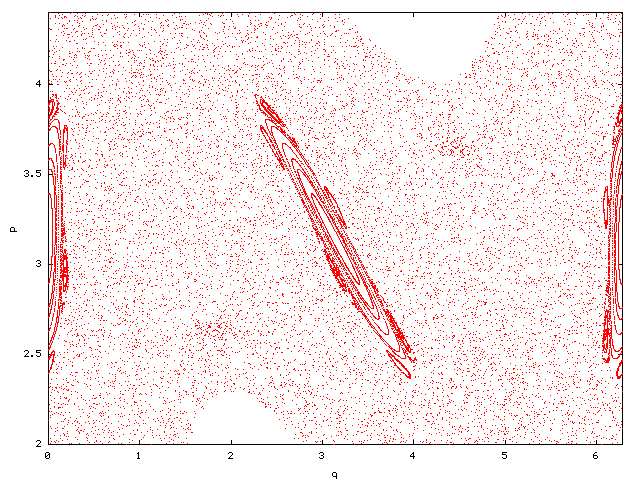
orbits around (pi,0) -> (pi,pi) for k=1.9

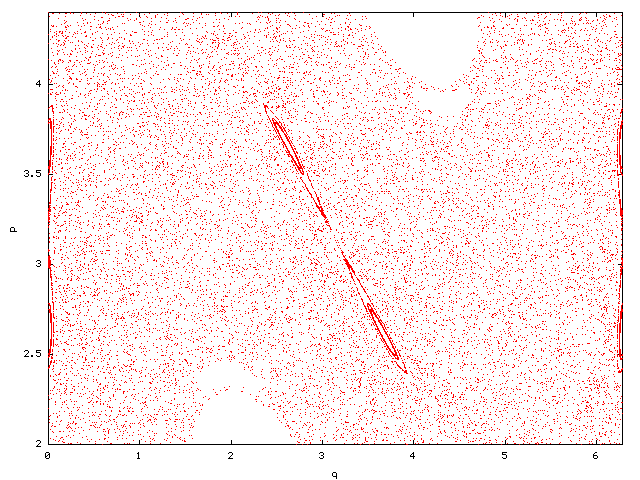
For k=2.1 it has become unstable, again by creating a stable periodic orbit with double period nearby (below).

orbits around (pi,0) -> (pi,pi) for k=2.1

Valid HTML 4.01! Last modified: Jun 06 2001
Stefan Keppeler ( stefan.keppeler@physik.uni-ulm.de)