Zusatz-Blatt C

Wer in der vorlesungsfreien Zeit die in der Vorlesung eingeführten Begriffe üben möchte, dem seien die im Folgenden angeführten Aufgaben empfohlen. Die Lösungen sind nicht abzugeben und werden auch nicht korrigiert. Sie werden aber auf Wunsch in den Tutorien besprochen!

VEKTORRÄUME UND MODULN

Aufgabe 1:    Es sei $(K,+,\cdot)$ ein Körper, $(V,+,\cdot)$ ein K-Vektorraum und $U,U'\subseteq V$ Unterräume von V. Zeige, genau dann ist $U\cup U'$ ein Unterraum von V, wenn $U\subseteq U'$ oder $U'\subseteq U$.

Aufgabe 2:    Es sei $V=\R^\R$ der $\R$-Vektorraum der Abbildungen von $\R$ nach $\R$. Welche der folgenden Teilmengen von V sind Unterräume von V? Beweise Deine Aussagen.

1.

$U_1:=\{f\in V\;\vert\; f(0)=2\}$,

2.

$U_2:=\{f\in V\;\vert\; f(1)=0\}$,

3.

$U_3:=\{f\in V\;\vert\; f\mbox{ ist beschränkt}\}$,

4.

$U_1:=\{f\in V\;\vert\; \vert f(x)\vert\leq 4\;\forall\;x\in\R\}$.

Aufgabe 3:    Welche der folgende Teilmengen von $\R^4$ sind Unterräume des $\R^4$? Begründe Deine Aussagen.

1.

$\{(1,0,0,0)^t,(0,1,0,0)^t,(1,1,0,0)^t,(0,0,0,0)^t\}$,

2.

$\{(x,0,0,0)^t,(0,y,0,0)^t\;\vert\;x,y\in\R\}$,

3.

$\{(x,x,y,y)^t\;\vert\;x,y\in\R\}$,

4.

$\{(x_1,x_2,x_3,x_4)^t\;\vert\;x_i\in\R, \sum_{i=1}^4x_1=1\}$,

5.

$\{(x_1,x_2,x_3,x_4)^t\;\vert\;x_i\in\R, \sum_{i=1}^4x_1=0\}$,

6.

Ist $\{(1,0,0,0)^t,(0,1,0,0)^t,(1,1,0,0)^t,(0,0,0,0)^t\}$ aufgefaßt als Teilmenge von $(\Z/2\Z)^4$ ein Unterraum des $\Z/2\Z$-Vektorraums $(\Z/2\Z)^4$?

Aufgabe 4:    Gib alle Elemente und alle Unterräume des $\Z/2\Z$-Vektorraums $(\Z/2\Z)^2$ an.

Aufgabe 5:    [Funktionenräume]
Es sei $V=C^\infty(\R)=\{f:\R\rightarrow\R\;\vert\;f \mbox{ ist unendlich oft differenzierbar}\}$ der $\R$-Vektorraum der unendlich oft differenzierbaren Funtionen auf $\R$. Zeige, die Abbildung $D:V\rightarrow V:f\mapsto f'$, wobei f' die Ableitung von f bezeichne, ist eine $\R$-lineare Abbildung.
Es gilt $\exp(x)=\sum_{n=0}^\infty\frac{x^n}{n!}\in V$. Folgt aus der Linearität von D, daß $D\big(exp(x)\big)=\sum_{n=0}^\infty D\big(\frac{x^n}{n!}\big)=exp(x)$?

Aufgabe 6:    Es seien $f,g\in\End_K(V)$, V ein K-Vektorraum, $0\not=\lambda\in K$. Zeige:

1.

$\im(f+g)\subseteq\im(f)+\im(g)$,

2.

$\Ker(f+g)\supseteq\Ker(f)+\Ker(g)$,

3.

$\im(\lambda f)=\im(f)$,

4.

$\Ker(\lambda f)=\Ker(f)$,

5.

$\im(f\circ g)\subseteq \im(f)$, und

6.

$\Ker(f\circ g)\supseteq \Ker(g)$.

Aufgabe 7:    Es sei V ein K-Vektorraum und $f\in\Hom_K(V,V)$. Zeige, für $m,n\in\N$ mit m<n gilt:

$$\Ker(f^m)\subseteq\Ker(f^n)\mbox{ and } \im(f^m)\supseteq\im(f^n).$$

Finde Beispiele, so daß die Inklusionen stets strikt sind.

Aufgabe 8:    Es seien U,V,W drei K-Vektorräume, $f\in\Hom_K(U,V)$ und $g\in\Hom_K(U,W)$. Zeige, genau dann gibt es ein $h\in\Hom_K(W,V)$ mit $h\circ g=f$, wenn $\Ker(g)\subseteq\Ker(f)$.

LINEARE ABHÄNGIGKEIT UND BASEN

Aufgabe 9:    Es sei V ein K-Vektorraum, $U\subset V$ ein Unterraum, $u\in U$ und $v\in V\setminus U$. Zeige, v und u sind linear unabhängig.

Aufgabe 10:    Es sei $(K,+,\cdot)$ ein Körper, $(V,+,\cdot)$ ein K-Vektorraum, und $v_1,\ldots,v_n\in V$ seien linear abhängige Vektoren mit der Eigenschaft, daß je n-1 der Vektoren linear unabhängig sind. Zeige:

1.

Es gibt $\lambda_1,\ldots,\lambda_n\in K\setminus\{0\}$ mit der Eigenschaft

$$\sum_{i=1}^n \lambda_i\cdot v_i=0.$$

2.

Gilt für $\mu_1,\ldots,\mu_n\in K$ ebenfalls $\sum_{i=1}^n \mu_i\cdot v_i=0$, so gibt es ein $\nu\in K$ mit $\mu_i=\lambda_i\cdot\nu$ für alle $i=1,\ldots,n$.

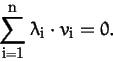
Aufgabe 11:    Es sei $V=K^\infty:=K^\N=\{(a_0,a_1,a_2,\ldots)\;\vert\; a_i\in K\;\forall\;i\in\N\}$ der K-Vektorraum aller Folgen über K mit komponentenweiser Addition und Skalarmultiplikation. Ferner sei $e_i\in V$ die Folge, die an i-ter Stelle eine Eins und sonst nur Nullen enthält. Ist dann $(e_i\;\vert\;i\in\N)$ eine Basis von V?

Aufgabe 12:     Es sei $V=\R^\R$. Für $k\in\N$ definiere $f_k:\R\rightarrow\R:x\mapsto\sin(kx)$ und $g_k:\R\rightarrow\R:x\mapsto\cos(kx)$. Zeige, $\big(f_k,g_k\;\vert\;k\in\N\big)$ ist eine (unendliche) linear unabhängige Familie im $\R$-Vektorraum $\R^\R$.

Aufgabe 13:    Es sei $V=\R^3$, $U=\{(x+y,y,y-x)^t\;\vert\;x,y\in\R\}$ und $U'=\{(x,y,z)^t\in\R^3\;\vert\;z=2x+y\}$. Bestimme Basen von U+U', $U\cap U'$, V/U und V/U'.

Aufgabe 14:    Ist U ein Unterraum des K-Vektorraums V und $M,N\subseteq V$.

1.

Gilt $V=\langle M\rangle$, dann gilt $V/U=\langle m+U\;\vert\;m\in M\rangle$.

2.

Gilt $V/U=\langle m+U\;\vert\;m\in M\rangle$ und $U=\langle N\rangle$, so gilt $V=\langle M\cup N\rangle$.

Aufgabe 15:     Seien V und W K-Vektorräume und $f:V\rightarrow W$ eine K-lineare Abbildung. Ferner sei $B=(v_i\;\vert\; i\in I)$ eine Basis von V und $F=(f(v_i)\;\vert\;i\in I)$. Zeige:

1.

f ist genau dann injektiv, wenn F linear unabhängig ist.

2.

f ist genau dann surjektiv, wenn $W=\langle F\rangle$.

Hinweis: Bei geschickter Vorgehensweise lassen sich Teil b. sowie eine Richtung von Teil mit jeweils einer Zeile beweisen! - Der Satz steht zwar in der Vorlesung, der Beweis ist aber als Übungsaufgabe gestellt.

ENDLICH-DIMENSIONALE VEKTORRÄUME

Aufgabe 16:    Es sei $U=\{(a_1,\ldots,a_5)^t\in\R^4\;\vert\;a_1-2a_2=0=2a_4+a_5\}\subset\R^5$. Bestimme die Dimension von U und sowie eine Basis, die den Vektor (2,1,1,-1,2)^t enthält.
Hinweis: Gauß und Steinitz!

Aufgabe 17:    Es sei $U=\langle (1,2,3,4)^t,(1,1,1,1)^t\rangle\subset \R^4$. Bestimme mit Hilfe des Austauschsatzes von Steinitz eine Basis von $\R^4/U$.

Aufgabe 18:    Es sei $K^\infty:=\{(a_i)_{i\in\N}\;\vert\;a_i\in K\}$ der K-Vektorraum aller Folgen im Körper K. Definiere Abbildungen $S,T:K^\infty\rightarrow K^\infty$ durch

$$S\big((a_i)_{i\in\N}\big)=(a_2,a_3,a_4,\ldots),$$

und

$$T\big((a_i)_{i\in\N}\big)=(0,a_1,a_2,\ldots).$$

1.

Zeige, S und T sind K-lineare Abbildungen.

2.

Bestimme $\Ker(S)$, $\im(S)$, $\Ker(T)$ und $\im(T)$.

3.

Überprüfe die Abbildungen auf Injektivität und Surjektivität.

4.

Bestimme die Komposita $S\circ T$ und $T\circ S$.

Aufgabe 19:    [Invariante Unterräume]
Es sei $U\subseteq V$ ein Unterraum des K-Vektorraums V, und $f\in\End_K(V)$ mit $f(U)\subseteq U$. Wir sagen dann, U ist f-invariant.
Definiere $f_U:U\rightarrow U$ durch f_U(x)=f(x) für alle $x\in U$, und $f_{V/U}:V/U\rightarrow V/U$ durch f_V/U(x+U)=f(x)+U für alle $x+U\in V/U$. Zeige:

1.

f_U und f_V/U sind K-lineare Abbildungen.

2.

$\Ker(f_U)=\Ker(f)\cap U$ und $\im(f_U)\subseteq\im(f)\cap U$.

3.

$\im\big(f_{V/U}\big)=\big(U+\im(f)\big)/U$.

4.

Falls $\dim(V)<\infty$, dann gilt

$$\rang\big(f_{V/U}\big)=\dim_K\big(\im(f)\big)-\dim_K\big(U\cap\im(f)\big) \leq \rang(f)-\rang\big(f_U\big).$$

5.

$\Ker\big(f_{V/U}\big)\supseteq\big(U+\Ker(f)\big)/U$.

6.

Falls $\dim(V)<\infty$, dann gilt

$$\dim_K\big(\Ker(f)\big)-\dim_K\big(\Ker(f_U)\big) \leq\dim_K\big(f_{V/U}\big)\leq\dim\big(\Ker(f)\big).$$

Aufgabe 20:    Es sei V ein (nicht-notwendig endlich-dimensionaler) K-Vektorraum, $f\in\End_K(V)$ und $U\subseteq V$ ein f-invarianter Unterraum. Zeige:

1.

Genau dann ist $\im\big(f_U\big)=\im(f)$, wenn $V=U+\Ker(f)$.

2.

Genau dann ist $\Ker\big(f_{V/U}\big)=0$, wenn $\Ker\big(f^2\big)=\Ker(f)$.

Aufgabe 21:    Es sei V ein (nicht-notwendig endlich-dimensionaler) K-Vektorraum, $\Char(K)\not=2$, und $f\in\End_K(V)$ mit $f^2=\id_V$. Zeige:

1.

$\im\big(f-\id_V\big)=\Ker\big(f+\id_V\big)$, und

2.

$V=\Ker\big(f-\id_V\big)\oplus \Ker\big(f+\id_V\big)$.

Aufgabe 22:    Es sei V ein K-Vektorraum mit $\dim_K(V)=5$, und U und U' Unterräume mit $\dim_K(U)=3$ und $\dim_K(U')=4$.

1.

Welche Werte kann $\dim_K(U\cap U')$ annehmen?

2.

Gib für jeden der Werte von $\dim_K(U\cap U')$ ein Beispiel (K,V,U,U') an.

DIREKTE SUMMEN UND QUOTIENTENRÄUME

Aufgabe 23:    Es seien $U=\langle (1,0,1,1)^t,(-1,1,0,0)^t\rangle\subset\R^4$ und $U'=\langle (1,0,1,0)^t,(1,1,1,1)^t\rangle\subset\R^4$. Zeige, $\R^4=U\oplus U'$.

Aufgabe 24:    Es sei $V=U_1\oplus U_2$ ein K-Vektorraum und $f\in\Hom_K(V,V)$ mit $f(U_i)\subseteq U_i$ für i=1,2. Zeige:

1.

$\im(f)=\im\big(f_{U_1}\big)\oplus\im\big(f_{U_2}\big)$.

2.

$\Ker(f)=\Ker\big(f_{U_1}\big)\oplus\Ker\big(f_{U_2}\big)$.

Aufgabe 25:    Sei V ein K-Vektorraum, $f:V\rightarrow V$ eine K-lineare Abbildung. Zeige, daß dann die folgenden Aussagen gleichwertig sind:

1.

$V=\Ker(f)\oplus\im(f)$,

2.

$V=\Ker(f) + \im(f)$,

3.

$\Ker(f)\cap\im(f)=\{0\}$,

4.

$\Ker(f^2)=\Ker(f)$.

5.

$\im(f^2)=\im(f)$.

Aufgabe 26:    Gib Beispiele $f,g\in\Hom_\R\big(\R^2,\R^2\big)$ an mit $\im(f)=\Ker(f)$ und $\R^2=\im(g)\oplus\Ker(g)$.

Aufgabe 27:    [Projektionen]
Es sei V ein K-Vektorraum. $f\in\End_K(V)$ heißt Projektion, falls f²=f gilt. Zeige, die folgenden Aussagen sind äquivalent:

1.

f ist eine Projektion,

2.

$\id_V-f$ ist eine Projektion,

3.

$\im\big(\id_V-f\big)=\Ker(f)$,

4.

$\Ker\big(\id_V-f\big)=\im(f)$.

Aufgabe 28:    Es sei V ein K-Vektorraum, $f,g\in\End_K(V)$. Ein Unterraum $U\subseteq V$ heißt g-invariant, falls $g(U)\subseteq U$. Zeige:

1.

Gilt $f\circ g=g\circ f$, so sind $\im(f)$ und $\Ker(f)$ g-invariant.

2.

Ist f eine Projektion und sind $\im(f)$ und $\Ker(f)$ g-invariant, so gilt $f\circ g=g\circ f$.

3.

Sind f und g Projektionen mit $f\circ g=g\circ f$, so gilt

(a)

$\im(f\circ g)=\im(f)\cap\im(g)$, und

(b)

$\Ker(f\circ g)=\Ker(f)\cap\Ker(g)$.

4.

Ist $V=U_1\oplus U_2=W_1\oplus W_2$ mit $U_1\subseteq W_2$ und $W_1\subseteq U_1$, so gilt

$$V=\big(U_1+W_1\big)\oplus\big(U_2\cap W_2\big).$$

Aufgabe 29:    Es seien $U,U'\subseteq V$ Unterräume des K-Vektorraumes V. Zeige:

1.

$(U+U')/U\cong U'/(U\cap U')$,

2.

Falls $U'\subseteq U$, dann gilt $(V/U')/(U/U')\cong V/U$.

LINEARE ABBILDUNGEN UND MATRIZEN

Aufgabe 30:    Es sei $B=\big((1,1,1,1)^t,(-1,0,0,1)^t,(0,-1,0,1)^t,(0,0,-1,1)^t\big)$ und $C=\big((1,1,0)^t,(0,1,1)^t,(0,0,1)^t\big)$.

1.

Zeige, B ist eine Basis des $\R^4$ und C eine Basis des $\R^3$.

2.

Für $f\in\Hom_\R\big(\R^4,\R^3\big)$ mit f(x₁,x₂,x₃,x₄)=(x₁-x₂,x₃,x₂+x₄)^t bestimme M_C^B(f).

3.

Bestimme umgekehrt die Funktionsvorschrift für $g\in\Hom_\R\big(\R^4,\R^3\big)$ mit

$$M_C^B(f)=\left(\begin{array}{rrrr}1&0&-1&0\\ 2&1&3&1\\ 0&-1&2&0\end{array}\right).$$

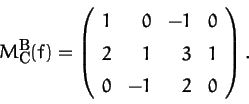
Aufgabe 31:    Es sei B=(v₁,v₂,v₃) eine Basis des K-Vektorraumes V, C=(w₁,w₂) eine Basis des K-Vektorraumes W und $f:V\rightarrow W$ sei eine K-lineare Abbildung, so daß M_B^C(f)=(a_i,j)_{i=1,2;j=1,2,3} die Matrix-Darstellung von f bezüglich B und C ist. Ferner setzen wir:

$$\begin{array}{l@{\hspace{2cm}}l} v_1'=v_1+v_2+v_3 & w_1'=w_2\\ v_2'=v_2+v_3 & w_1'=w_1-w_2\\ v_3'=v_3 & \\ \end{array}$$

und B'=(v₁,v₂,v₃) sowie C'=(w₁',w₂').

1.

Zeige, B' ist eine Basis von V und C' ist eine Basis von W.

2.

Bestimme, die Matrix M_B'^C'(f), d. h. die Matrix-Darstellung von f bezüglich der Basen B' und C'.

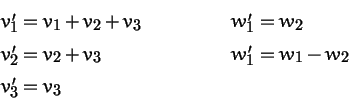
Aufgabe 32:    Es sei V ein $\R$-Vektorraum, B=(v₁,v₂,v₃) eine Basis von V und C=(w₁,w₂,w₃) mit w₁=v₁+v₃, w₂=v₁+v₂ und w₃=v₁+v₂+v₃.

1.

Zeige, C ist eine Basis von V.

2.

Bestimme M_C^C(f), wobei $f\in\End_\R(V)$ gegeben ist durch

$$M_B^B(f)=\left(\begin{array}{rrr}a&0&b\\ -b&a&a\\ a&b&b\end{array}\right), \mbox{ mit } a,b\in\R.$$

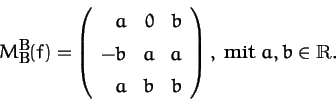
Aufgabe 33:    Es sei $V\not=\{0\}$ ein n-dimensionaler K-Vektorraum, und $f:V\rightarrow V$ sei K-linear. Zeige, die beiden folgenden Aussagen sind gleichwertig:

1.

Für je zwei Basen B und B' von V gilt:

M_B^B(f)=M_B'^B'(f).

2.

Es gibt ein $k\in K$ mit $A=k\cdot{\mathbbm 1}_n$.

Aufgabe 34:    Es sei R ein Ring, $A=\big(a_{ij}\big)_{i,j=1,\ldots,n}\in\Mat(n\times n,R)$ mit a_ij=0 für $i\geq j$. Zeige, Aⁿ=0.

Aufgabe 35:    Es sei $A\in\Mat(n\times n,K)$ mit AB=BA für alle $B\in\Mat(n\times n,K)$. Zeige, es gibt ein $a\in K$ mit $A=a\cdot{\mathbbm 1}_n$.

Aufgabe 36:    Es sei V ein K-Vektorraum, und $f,g\in\Hom_K(V,V)$ mit $\Ker(f)=0$ sowie $0\subsetneqq \Ker(g)\subsetneqq V$. Zeige, (f,g) ist eine linear unabhängige Familie im K-Vektorraum $\End_K(V)$.

Aufgabe 37:    Es sei V ein K-Vektorraum mit $\dim_K(V)=n\geq 1$. Ferner seien $f\in\End_K(V)$ und $v\in V$ mit:

(i)

$\big(v,f(v),\ldots,f^{n-1}(v)\big)$ ist eine linear unabhängige Familie in V, während

(ii)

$\big(f(v),f^2(v),\ldots,f^n(v)\big)$ linear abhängig ist.

Zeige, die Familie $\big(\id_V,f,f^2,\ldots,f^{n-1}\big)$ ist linear unabhängig im K-Vektorraum $\End_K(V)$.

LGS UND DER GAUSS'SCHE ALGORITHMUS

Aufgabe 38:    Bestimme, sofern sie existiert, die Inverse der Matrix

$$A=\left(\begin{array}{rrrr}2&-3&2&5\\ 1&-1&1&2\\ -3&2&2&1\\ 1&1&-3&-5\end{array}\right).$$

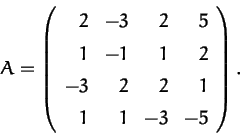
Aufgabe 39:    Es sei E die kanonische Basis des $\R^5$. Betrachte $f\in\End_\R\big(\R^5\big)$ mit

$$M_E^E(f)=\left(\begin{array}{rrrrr}0&1&1&1&1\\ -1&0&1&1&1\\ -1&-1&0&1&1\\ -1&-1&-1&0&1\\ -1&-1&-1&-1&0\end{array}\right).$$

1.

Bestimme eine Basis von $\Ker(f)$.

2.

Bestimme eine Basis von $\im(f)$.

Aufgabe 40:    Es sei $U=\langle(2,-1,1,-1)^t,(1,-2,2,1)^t,(3,-1,0,2)^t\rangle\subset\R^4$ und $U'=\langle(3,-2,3,8)^t,(2,1,-5,3)^t\rangle\subset\R^4$. Bestimme eine Basis von $U\cap U'$.

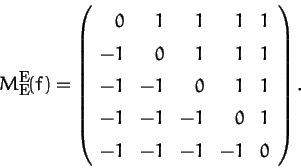
DETERMINANTEN

Aufgabe 41:    Für $n\in\N\setminus\{0\}$ definieren wir $A_n\in\Mat(n\times n,\R)$ als die Matrix, deren Eintäge auf der Diagonalen sowie auf der oberen und unteren Nebendiagonalen alle eins sind, während alle anderen Einträge null sind. Ferner setzen wir $d_n=\det(A_n)$.

1.

Zeige, für $n\geq 3$ gilt die Rekursionsformel d_n=d_n-1-d_n-2.

2.

Zeige, für $k\in\N$ gilt

$$d_n=\left\{\begin{array}{rl}1,&\mbox{ falls } n\equiv 1 (\mod... ...\mod 6)\mbox{ oder }n\equiv 4 (\mod 6). \end{array}\right.$$

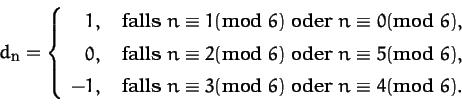
Aufgabe 42:    Für $t\in\R$ definiere $f_t\in\End_\R\big(\R^3\big)$ durch f(x,y,z)=(x+z,x+2y+z,tx+y-z)^t.

1.

Für welche $t\in\R$ ist f_t ein Automorphismus?

2.

Berechne in diesen Fällen f_t^-1 mit Hilfe der Adjungierten von M_E^E(f), wo E die kanonische Basis des $\R^3$ ist.

Aufgabe 43:    Es sei K ein Körper, $A\in\Mat(n\times n,K)$. Zeige:

1.

Ist $\Char(K)\not=2$, $n\equiv 1(\mod 2)$ und gilt falls A^t=-A, dann ist A nicht invertierbar.

2.

Ist $\Char(K)=2$, so gibt es zu jedem $0\not=n\in\N$ ein invertierbares A mit A^t=-A.

Aufgabe 44:    Es sei V ein $\R$-Vektorraum mit Basis B=(v₁,v₂) und $f\in\End_\R(V)$ sei gegeben mit f(v₁)=av₁+bv₂ und f(v₂)=-bv₁+av₂, wobei $a,b\in\R$ geeignet.

1.

Zeige, $\big(\id_V, T, T^2\big)$ ist eine linear abhängige Familie im $\R$-Vektorraum $\End_\R(V)$.

2.

Zeige, genau dann ist T ein Automorphismus, wenn $a^2+b^2\not=0$.

3.

Falls $a^2+b^2\not=0$, bestimme T^-1(v₁) und T^-1(v₂).

Aufgabe 45:    Es sei $V=\Mat(2\times 2,K)$, der Vektorraum der $2\times 2$-Matrizen über dem Körper K. Zu $A\in V$ assoziieren wir eine K-lineare Abbildung

$$T_A:V\rightarrow V: X\mapsto A\circ X.$$

Zeige:

1.

Für $A\in V$ ist $T_A\in\End_K(V)$.

2.

Genau dann ist $\det(A)\not=0$, wenn $\det\big(T_A\big)\not=0$.

3.

$\Spur\big(T_A\big)=2\Spur(A)$.

4.

$\alpha:V\rightarrow\End_K(V):A\mapsto T_A$ ist K-linear, d. h.  $\alpha\in\Hom_K\big(V,\End_K(V)\big)$.