


Next: About this document ...
Gauß-Algorithmus
INPUT:
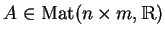 .
.
OUTPUT: Zeilen-Stufen-Form von A.
GROB-FASSUNG:
1. SCHRITT: Prüfe, ob A=0 . Falls ja,
gib Azurück. Falls nein, fahre mit 2. Schritt fort.
2. SCHRITT: Durchlaufe die Spalten von oben
nach unten, mit der ersten Spalte beginnend, bis der erste Eintrag
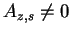 gefunden ist. Dies wird unser Pivot-Element.
gefunden ist. Dies wird unser Pivot-Element.
3. SCHRITT: Steht Az,s nicht in der
ersten Zeile, vertausche die Zeilen 1 und z.
4. SCHRITT: Mache alle Elemente in der Spalte
s unterhalb von A1,s zu Null durch elementare Umformungen
vom Typ III.
5. SCHRITT: Bezeichne mit A' den Block, der
entsteht, wenn wir die erste Zeile und die ersten s Spalten
streichen, und führe den gleichen Algorithums mit A' aus.
FEINERE FASSUNG:
Falls A=0,
Sonst
- Starte mit Zeile z=1 und Spalte s=1.
- Solange Az,s=0 und z<=m,
- Falls z<m,
- gehe eine Zeile weiter (d. h. erhöhe z um eins).
- Sonst,
- gehe eine Spalte weiter und beginne wieder mit der
ersten Zeile (d. h. erhöhe s um eins und setze z auf
eins).
Falls 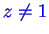 ,
,
- vertausche Zeile 1 mit Zeile z.
Für
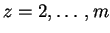 tue
tue
- z. Zeile := z. Zeile -
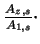 1. Zeile.
1. Zeile.
Falls noch nicht alle Zeilen / Spalten abgearbeitet
sind,
- Definiere A' als den Block, der entsteht, wenn man die
erste Zeile in A und die ersten s Spalten in A
streicht.
- Wende den Algorithmus auf A' an und setze das Ergebnis
(d. h. die ZFS von A') wieder in A ein.
Gib A zurück.
Die
Singular-Prozedur
proc gauss_lecture (matrix A)
"USAGE: gauss_lecture(A); A matrix
RETURN: matrix, A in Gauss normal form, i.e. row reduced
KEYWORDS: Gauss elimination, Gauss normal form, Gauss reduction
EXAMPLE: example gauss_lecture; shows an example"
{
int m=nrows(A); // Anzahl der Zeilen von A
int n=ncols(A); // Anzahl der Spalten von A
int z,s=1,1; // Zeilen-/Spaltenlaufindex
matrix Nullmatrix[m][n]=0;
// Überprüfe, ob A die Null-Matrix ist. Wenn ja, gib sie zurueck ...
if (A==Nullmatrix)
{
return(A);
}
// ... wenn nein, können wir ein Privot-Element finden.
else
{
// Suche ein Pivot-Element, mittels spaltenweisem Prüfen der Elemente.
while ((z<=m) and (A[z,s]==0))
{
// Suche in der s-ten Spalte das erste Element ungleich Null.
if (z<m)
{
z=z+1;
}
// Wenn in s. Spalte keins ist, dann gehe in die (s+1) Spalte.
else
{
z=1;
s=s+1;
}
}
// Das Pivot-Element ist nun A[z,s], also vertausche s. und 1. Zeile.
if (z!=1)
{
A=permrow(A,1,z);
}
// Reduziere die 2. bis m. Zeile mit der ersten.
for (int k=2;k<=m;k++)
{
A=addrow(A,1,-A[k,s]/A[1,s],k);
}
// Wende das gleiche Verfahren auf den Block an, der durch Streichen
// der ersten Zeile und der ersten s Spalten entsteht, sofern der
// Block nicht leer ist.
if ((m>1) and (n>s))
{
matrix B[m-1][n-s]=A[2..m,s+1..n];
A[2..m,s+1..n]=gauss_lecture(B);
}
return(A);
}
}
example
{
"EXAMPLE:";
echo=2;
ring r=0,(x),lp;
matrix A[3][4]=1,2,3,4,5,6,7,8,9,10,11,12;
print(A);
print(gauss_lecture(A));
}
Alternativ eine Kurzfassung der Prozedur
proc gauss_recursive (matrix A)
{
int m,n,z=nrows(A),ncols(A),1;
while ((z<m) and (A[z,1]==0)){ z=z+1; }
if (A[z,1]!=0)
{
A=permrow(A,1,z);
for (int k=2;k<=m;k++){ A=addrow(multrow(A,k,A[1,1]),1,-A[k,1],k); }
}
if ((m>1) and (n>1))
{
if (A[1,1]!=0)
{
matrix B[m-1][n-1]=A[2..m,2..n];
A[2..m,2..n]=gauss_recursive(B);
}
else
{
matrix B[m][n-1]=A[1..m,2..n];
A[1..m,2..n]=gauss_recursive(B);
}
}
return (A);
}



Next: About this document ...
Thomas Keilen
1999-11-16
![]() .
.
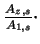 1. Zeile.
1. Zeile.