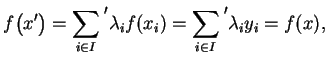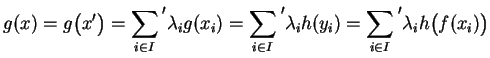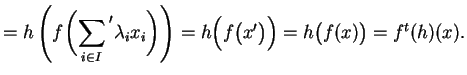1. Fehler:
Die Aussage 5.1.3 Teil 4 aus der Vorlesung ist falsch. Es gilt wohl,
wenn ![]() ein Isomorphismus ist, dann ist auch
ein Isomorphismus ist, dann ist auch ![]() ein
Isomorphismus - und der Beweis dafür ist auch richtig. Die
Umkehrung gilt i. a. jedoch nicht. Insbesondere
geht der Beweis nicht analog. Siehe dazu folgendes Beispiel.
ein
Isomorphismus - und der Beweis dafür ist auch richtig. Die
Umkehrung gilt i. a. jedoch nicht. Insbesondere
geht der Beweis nicht analog. Siehe dazu folgendes Beispiel.

Man beachte, daß im Fall, daß ![]() und
und ![]() endlich-dimensionale
endlich-dimensionale
![]() -Vektorräume sind, sehr wohl gilt,
-Vektorräume sind, sehr wohl gilt, ![]() ist ein Isomorphismus,
genau dann, wenn
ist ein Isomorphismus,
genau dann, wenn ![]() ein Isomorphismus ist, da dann ja
ein Isomorphismus ist, da dann ja
![]() .
.
2. Fehler:
Es steht noch der Beweis der Aussage
Sei also
![]() . Wir suchen ein
. Wir suchen ein ![]() mit
mit
![]() .
.
Schritt a.: Wir wählen nun eine Basis
![]() von
von ![]() und ergänzen diese zu einer Basis
und ergänzen diese zu einer Basis
![]() von
von ![]() . Sodann wählen wir zu jedem
. Sodann wählen wir zu jedem ![]() ,
, ![]() , ein
, ein
![]() , und definieren eine
, und definieren eine ![]() -lineare Abbildung
-lineare Abbildung
![]() durch
durch
![$\displaystyle h:W\rightarrow K:\left\{
\begin{array}[m]{ll}
y_i\mapsto g(x_i)\in K,&i\in I,\\
z_j\mapsto 0\in K,& j\in J.
\end{array}\right.
$](img20.gif)
Schritt b.: Wir zeigen nun, daß ![]() .
.
Sei dazu ![]() . Dann gibt es
. Dann gibt es
![]() ,
, ![]() , mit
, mit
![]() .
Dann gilt aber für
.
Dann gilt aber für
![]() ,
,