Groups and Representations
Objectives
- To know basic concepts of group and representation theory.
- To be able to explain proofs learned in the lectures and use methods and results in order to solve exercises. To be able to apply representation theory also in novel contexts.
- To know examples for the application of group representations in physics.
Contents
- groups: subgroups, homomorphisms, isomorphisms, group actions, orbits, stabilisers, equivalence classes, normal subgroups, cosets, factor groups
- representations (reps): faithful reps, unitary reps, irreducible reps (irreps), reducibility, characters, Schur's lemma(s), orthogonality of irreps
applications: symmetries and degeneracies in quantum mechanics, selection rules - representations of finite groups: group algebra, regular representation, ideals, idempotents
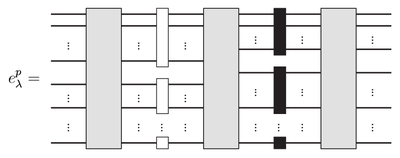
- symmetric groups: Young tableaux, Young operators, dimensions and characters
application: identical particles in quantum theories - Lie groups: Haar measure, representations, Lie algebras
- tensor reps of classical groups: symmetry classes, Young tableaux
applications: SU(2) and SU(3) in particle physics (spin, isospin, flavour) - maybe: irreps of the Lorentz and Poincaré groups
application: notion of particles in quantum theories - maybe: roots and weights; Killing-Cartan classification of semi-simple Lie algebras
Registration
Please register for the exercises on URM.
Summaries
In summer 2021, the course was taught in a flipped classroom format. The instructions from summer 2021 with their links to short videos can now be used as summaries or review material.
Discord Server
We have our own Discord server for this course. You find the invitation link on Ilias (access with zdv login). Feel free to discuss course related questions or the homework problems here with your fellow students. Your course instructors will also give advice or answer questions. If we happen to effectively solve a homework problem through discussion on Discord that's fine.
Literature
Note: You do not need to buy a specific book for this course. You should work with your notes. Check out the books for additional information or alternative presentations. Do not buy any book unless you already know that you like it and that you can work with it.
- Irene Verona Schensted, A course on the Application of Group Theory to Quantum Mechanics, NEO Press, 1976.
- Barry Simon, Representations of Finite and Compact Groups, American Mathematical Society, 1996.
- Wu-Ki Tung, Group Theory and Physics, World Scientific, 1985.
- William Fulton and Joe Harris, Representation Theory - A First Course, Springer-Verlag, 1991.
- Predrag Cvitanović, Group Theory - Birdtracks, Lie's and Exceptional Groups, Princeton University Press, 2008, http://birdtracks.eu/.
