Fachbereich Mathematik

Mathematik 1 für Naturwissenschaftler*innen

Veranstaltungsbeginn: Mi 16.10.24, 10:15 (N7)
Wir besprechen gemeinsam den Veranstaltungsmodus. Dann schauen wir uns eine hübsche Gleichung an.

Übungsbetrieb: Bitte melden Sie sich so bald wie möglich für die Übungen an.

FAQ

xkcd_2889_greenhouse_effect.png
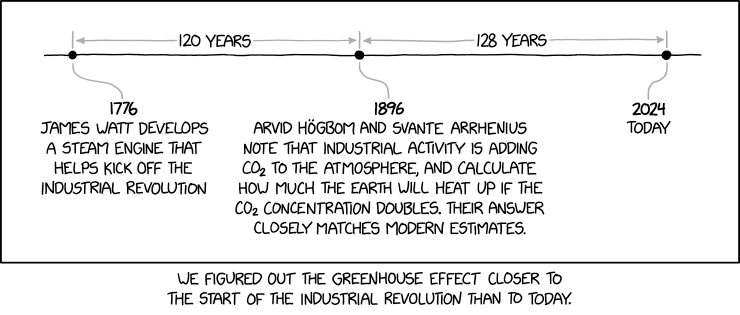
xkcd.com/2889 licensed under CC BY-NC 2.5

    Lernziele

        • Die Student*innen kennen grundlegende Methoden und Prinzipien der höheren Mathematik.
        • Sie wenden diese Methoden sicher in expliziten Aufgaben an.
        • Sie verstehen in Grundzügen, warum die erlernten Methoden funktionieren und kennen insbesondere die Voraussetzungen für ihre Anwendbarkeit.

    Inhalte

          • vollständige Induktion, geometrische Reihe, binomische Formel,
          • Grenzwerte, Stetigkeit, Differentiation, Potenzreihen,
          • Vektorräume, lineare Gleichungssysteme, Skalarprodukte, Normen,
          • Matrizen, Determinanten,
          • Komplexe Zahlen,
          • Integration.

        Leistungsnachweis (Schein/Note)

            • Ausschlaggebend ist das Ergebnis der Klausur am Mi 12.02.25, 8:30-10:30.
              Erlaubtes Hilfsmittel: Ein beidseitig handbeschriebenes A4-Blatt (kein Taschenrechner).
            • Voraussetzung für die Klausurteilnahme ist die erfolgreiche Teilnahme an den Übungen (d.h. mindestens 50% der Punkte sowie aktive Mitarbeit in der Übungsgruppe). Der aktuelle Punktestand ist auf https://urm.math.uni-tuebingen.de einsehbar.
            • Sollten Sie die Klausur nicht bestehen, so wird am Di 15.04.25, 16:30-18:30, eine Nachklausur angeboten.

        Anmeldung für die Übungen

        Die Übungsanmeldung ist abgeschlossen.

        Übungsgruppen

        Es finden folgende Übungsgruppen statt. Die Gruppeneinteilung wurde per Email versandt, siehe auch https://urm.math.uni-tuebingen.de.

        1 Mo 9-11 S11 Leander Maier
        2 Mo 16-18 8D09 Joana Werner Pinto
        3 Mo 16-18 N16 Tobias Nico Dürr
        4 Di 10-12 8D09 Florian Babisch
        5 Di 16-18 C9A03 Sebastian Queisser
        6 Mi 14-16 A3M04 Ellen Diez
        7 Mi 18-20 C9A03 Sina Hemmecke
        8 Do 10-12 D8H33 Julia Geißert
        9 Do 10-12 8D09 Louis Tolvig
        10 Do 12-14 N12 Almut Lemke
        11 Do 12-14 N15 Luis Berger

        Khan-Codes und weitere Infos zu den Übungsgruppen finden Sie in Ilias.

        Discord-Server
        Wir haben einen Discord-Server zur Lehrveranstaltung angelegt. Dort können Sie sich untereinander über Vorlesungsthemen, Lösungsansätze für Übungsaufgaben o.ä. austauschen. Zusätzlich sind auch alle Übungsgruppenleiter*innen und der Dozent mit dabei. Einen Einladungslink für den Discord-Server finden Sie auf Ilias (Zugang mit ZDV-Login).

        Zusammenfassungen
        Im WS 21/22 fand die Veranstaltung im Flipped-Classroom-Format statt. Die Anleitungen aus dem WS 21/22 mit ihren Links zu kurzen Videos können jetzt sehr gut als Zusammenfassungen oder Wiederholungsmaterial benutzt werden.

        TIMMS-Aufzeichungen
        Die Vorlesung wurde im Wintersemester 17/18 von timms (zdv) aufgezeichnet. Die Videos finden Sie auf dem Tübinger Internet MultiMedia Server.

        Aufgabe der Woche
        Auf Vorschlag rechne ich gerne gelegentlich eine Beispielaufgabe in einem Video vor, Channel:

        youtube_logo.png Mathematik für Naturwissenschaftler*innen

        Die folgende Playlist enthält Videos aus verschiedenen Wintersemestern:

        youtube_logo.png Mathe I

        Math Hour
        Neben der Betreuung durch Ihren Dozenten und Ihre Übungsgruppenleiter*innen in der Vorlesung, in den Übungsgruppen und im Webforum erhalten Sie auch zusätzliche Unterstützung in der Math Hour, der Mathematik-Sprechstunde für alle Studierenden der Mathematisch-Naturwissenschaftlichen Fakultät. An vier wöchentlichen Terminen helfen hier mehrere Betreuer*innen bei mathematischen Verständnisproblemen. Sie dürfen sich aber auch außerhalb der Vorlesungs- und Übungszeiten gerne an Ihre Übungsgruppenleiter*innen und an Ihren Dozenten wenden - wir freuen uns ebenfalls, wenn wir Ihnen weiterhelfen können.

        Die Facebook-Seite rund um die Lehrveranstaltung:

        facebook_logo.png Mathematik für Naturwissenschaftler/innen

        (Alle notwendigen Informationen zur Lehrveranstaltung erhalten Sie auch hier auf der Vorlesungshomepage, ganz ohne Facebook-Account.)

        Literaturangaben

        • Ich empfehle:
          K. Meyberg und P. Vachenauer: Höhere Mathematik 1 + 2. Springer.
          (knapp, präzise, im typischen Stil einer Uni-Mathevorlesung gehalten)
        • Auch geeignet erscheint mir:
          T. Arens, F. Hettlich, Ch. Karpfinger, U. Kockelkorn, K. Lichtenegger und H.Stachel: Mathematik. Spektrum Akademischer Verlag.
          (mehr Text, eher im Stil eines Schulbuchs gehalten)
        Andere Bücher mit entsprechendem Titel und Inhalt sind natürlich ebenfalls zur begleitenden Lektüre geeignet.

        Wichtig: Kaufen Sie keine (vielleicht teuren) Bücher, die Sie noch nicht kennen. Leihen Sie sich Bücher immer zunächst aus der Bibliothek aus, um zu sehen, ob Sie mit ihnen arbeiten können. Die Meisten sind in dieser Vorlesung ohnehin ganz ohne ergänzendes Buch erfolgreich.

        Wenn Sie feststellen, dass es gut wäre, die Schulmathematik etwas aufzufrischen:
        • Viel Material, wunderschön in kleinen Häppchen aufbereitet, bietet die Khan Academy. Hier können Sie zu allen Themen der Schulmathematik Videos mit Erklärungen und vollständig gelösten Beispielaufgaben anschauen. Und vor allem gibt es zum Üben einfache Rechenaufgaben, deren Ergebnisse sofort überprüft werden. Hinweis: Bevor Sie anfangen, im großen Stil Aufgaben zu lösen, machen Sie sich bitte dort einen Account. Sie werden damit voraussichtlich im Laufe des Semesters Zusatzpunkte sammeln können.