Fachbereich Mathematik

Proseminar Hyperbolische Geometrie

Wintersemester 2024/25

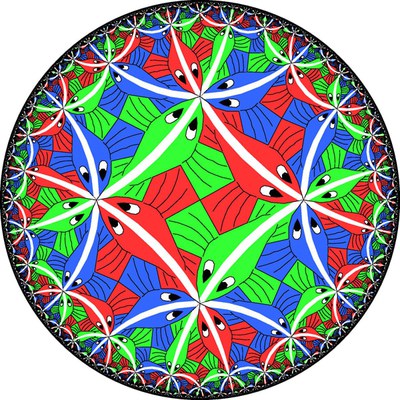
  • Thema: Während die Euklidische Geometrie (Anschauungsebene) die konstante Krümmung 0 hat und die Sphäre die konstante Krümmung 1, hat die hyperbolische Geometrie die konstante Krümmung -1. Anders als die Sphäre lässt sie sich aber nicht im Euklidischen Raum einbetten, deshalb erfodert die hyperbolische Geometrie größere Anstrengung unserer Phantasie. In der hyperbolischen Ebene gibt es z.B. Fünfecke mit 5 rechten Winkeln. Die hyperbolische Geometrie, auch unter dem Namen "nicht-Euklidische Geometrie" bekannt, wurde auf axiomatischem Weg entdeckt, wir werden aber hauptsächlich von ihrer Einbettung im Minkowski-Raum (R3 mit "Skalarprodukt" (x,y) = x1y1+x2y2-x3y3) ausgehen. Die Figur (nach einer Zeichnung des Künstlers M.C.Escher) zeigt eine Karte der hyperbolischen Ebene, die ebenso verzerrt ist wie Karten der Sphäre (z.B. Weltkarten); tatsächlich sind alle Fische gleich groß.

escher-H2.jpg

  • Leitung: Prof. Dr. Roderich Tumulka, Viet Hoang, Karla Schön
  • Sprache: deutsch
  • Studiengänge: B.Ed. und B.Sc. Mathematik.
  • Vorkenntnisse: Analysis 1 und Lineare Algebra 1 sind erforderlich. Analysis 2 und Geometrie sind hilfreich.
  • Vorträge: je 90 Minuten, ein Vortrag pro Woche
  • Vorläufiger Plan der Vorträge:

    Datum Sprecher Titel
    14.10. M. Hipp Quadratische Formen
    (Aufschrieb)
    21.10. S. Siegel Satz von Sylvester
    (Aufschrieb)
    28.10. L. Berger Lorentz-Gruppe
    (Aufschrieb)
    4.11. M. Kress Isometrien im Euklidischen Raum
    (Aufschrieb)
    11.11. C. Kilic Sphärische Geometrie
    (Aufschrieb)
    18.11. Ü. Koc Definition der hyperbolischen Geometrie
    25.11. T. Waffenschmidt Physikalische Bedeutung
    2.12. F. Haradinaj Geodätische in der hyperbolischen Ebene
    9.12. E. Wiebach Riemann-Metrik
    16.12. T. Magalhaes Hyperbolische Unterräume
    13.1. L. Brodbeck Karten von Klein und Poincaré
    20.1. T. Müller Isometrien der hyperbolischen Ebene
    27.1. T. Stetter Das rechtwinklige Fünfeck und andere Polygone
    3.2. L. Burkhardt Geschichte und Axiome der hyperbolischen Geometrie
  • Literatur: B. Iversen: Hyperbolic Geometry. London Mathematical Society (1992) (gibt es nur auf englisch)
    Literaturhinweise zu jedem Thema
  • Anmeldung: Die Anmeldung zu dieser Veranstaltung ist bereits geschlossen.