Computeralgebra

In kaum einem Bereich des täglichen Lebens kommt man heute mehr ohne Computer aus. Sein Siegeszug begann als Ersatz des Rechenschiebers z.B. in Form des Taschenrechners bei numerischen Berechnungen, d.h. bei solchen, bei denen die vorkommenden Zahlen gerundet werden. Doch darauf ist sein Einsatz inzwischen längst nicht mehr beschränkt; selbst die Arbeit mit komplizierten abstrakten Konzepten kann mittlerweile durch den Computer unterstützt werden. Damit hat der Computer auch Einzug gehalten in die Gebiete der 'reinen' Mathematik, wie etwa der Algebra, deren Begriffswelt geprägt ist von Abstraktion und von exakten (d.h. nicht gerundeten) symbolischen Operationen.

Ein Ziel der Computeralgebra ist es, exakte algebraische Methoden als Algorithmen zu formulieren und sie dadurch der Implementierung auf einem Computer zugänglich zu machen. Typisch hierbei ist, daß nicht so sehr das Rechnen mit Zahlen im Vordergrund steht, als vielmehr der effektive Umgang mit komplexeren algebraischen Strukturen wie z.B. Gruppen und Ringen. Denn gerade darin liegt der theoretische Wert einer solchen Behandlung eines algebraischen Problems: Die algorithmische Formulierung eines mathematischen Sachverhaltes ermöglicht wiederum neue Experimente auf höherem Niveau, deren Ergebnisse ihrerseits Anlaß zu neuen mathematischen Vermutungen geben und damit den Weg zu neuen mathematischen Erkenntnissen weisen können. Doch auch für praktische Anwendungen in Naturwissenschaft und Technik ist die Bedeutung der Computeralgebra nicht zu unterschätzen.

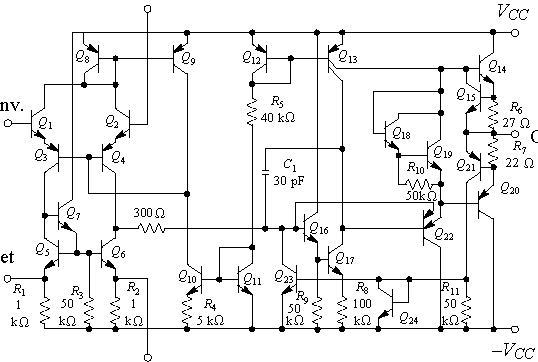
Abbildung 1: Der Einsatz von Computeralgebra beim Entwurf analoger elektronischer Schaltungen kann Entwurfszyklen reduzieren und einsparen helfen. Zudem kann die Entwurfssicherheit erhöht und die Entwicklungsdauer verkürzt werden, da symbolische Verfahren im Gegensatz zur numerischen Netzwerksimulation einen transparenteren Einblick in das Schaltungsverhalten vermitteln.

Lehre

So vielfältig wie die Anwendungen der Computeralgebra innerhalb der Mathematik ist auch das Wissen, das einem Studenten während seines Studiums vermittelt wird, falls er dieses Gebiet als seine Vertiefungsrichtung wählt. Deshalb haben sich die Arbeitsgruppen Algebraische Geometrie, Singularitätentheorie und Computeralgebra zu einem Vertiefungsgebiet zusammengefunden, in dem die Vorlesungen und Seminare eng aufeinander abgestimmt sind. So wird den Studenten ein optimaler Einstieg in dieses komplexe Gebiet ermöglicht, bei dem theoretische und praktische Komponenten eng miteinander verzahnt sind. Dabei ist die Anwendung mathematischer Software integraler Bestandteil der Ausbildung; Ziel ist die Durchdringung theoretischer Begriffe mit algorithmischem Verständnis bis hin zur praktischen Anwendung. Durch die Verwendung symbolischer Verfahren der Computeralgebra kann dies ohne Verzicht auf mathematische Exaktheit geschehen.

Da andererseits heute in fast jedem Gebiet der Mathematik Computeralgebra-Systeme, meist aus dem Bereich der sogenannten 'general purpose' Systeme wie etwa Maple oder Mathematica, zum Einsatz kommen, sollten auch Studenten mit anderen Vertiefungsrichtungen während ihres Studiums einen Einblick in die Theorie und Praxis dieses Gebietes erhalten, um später bei konkreten Fragestellungen die Chancen des flankierenden Einsatzes algebraischer Methoden nutzen zu können.

Gerade in der Lehrerausbildung gewinnt eine fundierte Basis an Computeralgebra in Zukunft immer mehr an Bedeutung, bedingt durch die rasante Entwicklung moderner Computeralgebra-Systeme. Durch die zunehmende Verfügbarkeit solcher Systeme zu oft moderaten Preisen werden auch Schüler demnächst vermehrt Zugang zu solcher Software haben und es stellt sich an Lehrer die neue Herausforderung diese kompetent und sinnvoll in ihren Unterricht zu integrieren. Dies kann nur gelingen, wenn er selbst einmal (zumindest exemplarisch) Einblick in die Funktionsweise solcher Algorithmen erhalten hat.

Ein besonderer Vorteil der Computeralgebra-Ausbildung in Kaiserslautern liegt darin, daß hier nicht nur theoretische Forschung in Computeralgebra und Einsatz von Computeralgebra Systemen stattfinden, sondern in dieser Gruppe auch ein Computeralgebra System entwickelt wird: SINGULAR.

Computeralgebrasystem SINGULAR

Viele bekannte Computeralgebra-Systeme, wie z.B. die oben bereits genannten Maple und Mathematica, vereinigen in sich eine große Zahl von Verfahren aus den verschiedenesten Teilgebieten der Mathematik und stellen damit für Mathematiker wie auch Naturwissenschaftler und Ingenieure ein wichtiges Werkzeug dar. Sie können aber nicht auf jedem dieser Gebiete bis ins letzte Detail optimiert sein - dazu ist die Vielfalt der Gebiete und Anwendungen viel zu groß. Ein Gegengewicht zu diesen sogenannten 'general purpose computer algebra systems' bilden spezialisierte Systeme, die meist aus konkreten Bedürfnissen der Forschung entstanden sind.

Solch ein Paket ist das in dieser Arbeitsgruppe entwickelte SINGULAR, ein System für polynomiale Berechnungen, das ursprünglich zur Behandlung bestimmter Fragestellungen aus der Singularitätentheorie entstand, da diese Fragestellungen 1986 weder theoretisch noch (mit den zur Verfügung stehenden Systemen) rechnerisch bewältigt werden konnten. Als Krönung dieser ersten Phase der Entwicklung konnten Vermutungen mittels auf dem Computer generierter Gegenbeispiele widerlegt werden, was wiederum die weitere theoretische Entwicklung beeinflußte.

Inzwischen ist SINGULAR zu einem der umfangreichsten und effizientesten Spezialsysteme gereift, mit dem man nicht nur polynomiale Gleichungssysteme lösen, sondern auch viele Berechnungen aus dem Bereich der Algebraischen Geometrie durchführen kann. Es findet in über 30 Ländern Anwendung, darunter auch in den USA und Japan. Als einziges System ist SINGULAR in der Lage die Lösungsmenge polynomialer Gleichungssysteme effizient in Singularitäten zu analysieren, d.h. in Punkten, in denen die Lösungsmenge nicht glatt, sondern z.B. verzweigt ist.

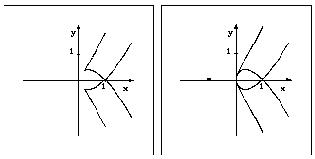
Abbildung 2,links: rein numerische Bestimmung der Lösungsmenge; rechts: bei vorheriger Analyse der Singularitäten mit SINGULAR.

Forschung

Eine zentrale Rolle in der Behandlung polynomialer Systeme spielen sogenannte Standard-Basen, die durch den Buchberger Algorithmus berechnet werden können; sie stellen eine besondere Form eines solchen Systemes dar, aus der man z.B. leichter Informationen über die Lösungsmenge ablesen kann. Da die Berechnung solcher Standard-Basen für praxisrelevante Systeme jedoch sehr zeit- und speicherintensiv sein kann, ist es von großer Bedeutung, nicht nur die vorhandenen Algorithmen optimal zu implementieren, sondern auch nach neuen Variationen der Methoden zu suchen (Forschungsthemen: p-modulare Standardbasen Berechnung, Gröbner Walk). Außerdem weist diese Behandlung polynomialer Systeme den Weg auch zur Bearbeitung verwandter Fragestellungen (Forschungsthemen: nicht-kommutative Standard-Basen, Verhalten von Standard-Basen unter Deformation, Standard-Basen für sogenannte Mikrolokale Strukturen).

Doch auch die Anwendung sowohl in der mathematischen als auch in der natur- und ingenieurwissenschaftlichen Forschung trägt stets neue Anforderungen und Probleme an die Computeralgebra heran.

Computeralgebra-Einsatz in Forschung und Anwendungen

• Kommutative Algebra und Algebraische Geometrie: Primärzerlegung, Kohomologieberechnung, Invariantenringe, ganzer Abschluß,...
  

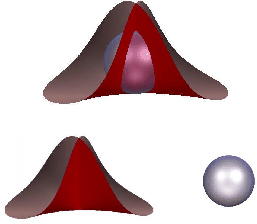
  Abbildung 3: Durch Primärzerlegung ist es möglich, diese Zerlegung der oberen Fläche in ihre Einzelteile (darunter) aus den Gleichungen zu berechnen, die die Fläche bestimmen.

• Singularitätentheorie: Bestimmung der singulären Punkte, numerische Invarianten für gegebene Beispiele, Monodromie, Verhalten unter Deformation, ...
  

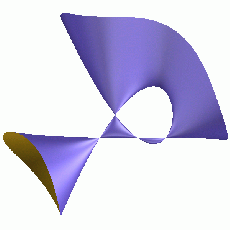
  Abbildung 4: Diese Fläche hat 4 singuläre Punkte; sie können mit Hilfe des Computers bestimmt werden

• praktische Anwendungen:
  • Glasschmelzen - Bestimmung optimaler Konzentrationen der Ausgangsbestandteile
    

    Abbildung 5: geschmolzenes Glas

• Elektrotechnik - Dimensionierung analoger Schaltungen, Robotik
  

  Abbildung 6: zu steuernder Roboterarm

• Chemie - Bestimmung möglicher Strukturen von Cycloheptan
  

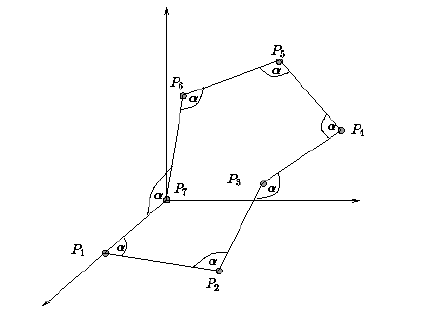
  Abbildung 7: Diese Skizze zeigt die zu bestimmende Anordnung sowohl für die Bewegung des Roboterarms als auch für die Struktur des Cycloheptan-Moleküls. Im ersten Fall muß cos(a)=0 gelten, im zweiten cos(a)=1/3. Dies ist ein Beispiel dafür, daß dasselbe Modell durchaus für sehr unterschiedlich anmutende technische Fragestellungen anwendbar sein kann und wie wichtig deshalb die mathematische Abstraktion ist.