The Berry-Keating operator on a lattice

Jens Bolte, Sebastian Egger, Stefan Keppeler

J. Phys. A 50 (2017) 105201
[doi:10.1088/1751-8121/aa5844 |arXiv:1610.06472]

Abstract

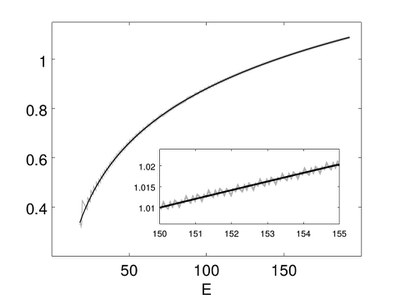
We construct and study a version of the Berry-Keating operator with a built-in truncation of the phase space, which we choose to be a two-dimensional torus. The operator is a Weyl quantisation of the classical Hamiltonian for an inverted harmonic oscillator, producing a difference operator on a finite, periodic lattice. We investigate the continuum and the infinite-volume limit of our model in conjunction with the semiclassical limit. Using semiclassical methods, we show that a specific combination of the limits leads to a logarithmic mean spectral density as it was anticipated by Berry and Keating.